TECNOLOGIA DE RELOJOARIA

 Post Fev. 08,12

CALCULO DE UMA RODA PERDIDA – Transmissão

Em 6.1 mostrámos como calcular o número de dentes duma roda perdida, do sistema da minuteria. Hoje vamos  calcular o número de dentes  de uma roda perdida, no sistema de transmissão. Isto é entre a roda do centro e a roda de escape.

Em primeiro lugar, convém lembrar que, na generalidade,  quando se perde uma roda perde-se igualmente o carreto que está no eixo dessa roda. Desta forma, no  processo de cálculo   passamos a ter duas incógnitas ( número de dentes da roda e do carreto ) e não uma.

Como dados da equação devemos conhecer:

              1- Número de dentes  de todas as restantes rodas e carretos

              2-As semi oscilações  por hora que o relógio  deve fazer ;  s/osc/h ou o comprimento do pendulo

Lembrando o “ post “ de Fev.4,12 temos:  s/osc/h = Z1 x Z2 x Z3 x Z4 x 2 : z2 x z3 x z4. Esta é uma formula geral, que deve ser adaptada em função do número de rodas que constituem o trem de engrenagem. Na verdade as oscilações  dos relógios de pêndulo são bastante mais lentas do que os relógios com  volante, pelo que em geral  têm menos uma roda. 

Vamos então,  supor que temos um relógio carrilhão, de parede, para  reparar mas que lhe falta  a roda  intermediária – Z2,  colocada ente a roda do centro e a roda de escape ( esta roda também é conhecida por roda terceira) e que,  com a roda,  se perdeu também o carreto- z2,   colocado no eixo da roda. Temos então duas incógnitas para resolver:

a) Calcular o número de dentes da roda

b) Calcular o número de dentes do carreto 

Contamos os  dentes das rodas existente e encontramos:

       Roda do Centro  ( Z1 ) igual a 96

       Roda intermediária ( Z2 )  ?  

       Roda de escape ( Z3 ) igual a 30

       Carreto de z2 ?

       Carreto da roda de escape z3 igual a  8

Porque sabemos o número das s/osc/h =  6480  podemos escrever que

Adaptando a formula geral a este caso temos:  s/osc/h = Z1 x Z2 x Z3 x 2 : z2 x z3

Ou

Z2:z2  = s/osc/h x z3  :  Z1  x Z3 x 2  

Porque sabemos o número das s/osc/h =  6480   vamos substituir  as letras pelos números correspondentes  e passamos a ter :

Z2:z2 :  6480 x 8 : 96 x 30 x 2  =  9:1

Isto é obtivemos a relação  que existe entre os dentes da roda e dos seu  carreto o que nos permite especular  que  os números mais prováveis  da roda  serão:  63, 72 ou 81 e que os dentes do carreto serão 7, 8 ou 9.

P - Como resolver esta dúvida ?

R – Pelo conhecimento  das distâncias  de entre centros com que a roda e o carreto engrenam e pelo conhecimento  do módulo dos dentes existentes . Este conhecimento vai-nos permitir  calcular os diâmetros totais  da roda e do carreto e assim identificar quais os números exactos  de dentes da roda e do carreto, que procuramos.

Outra das dúvidas que se coloca com regularidade e sobre o conhecimento das  s/osc/h. na verdade   não é  muito comum conhecer-se este dado, quando se repara um relógio .

P – Como  podemos   determinar as s/osc/h  de um relógio ?

R-  Se  tivermos  o pêndulo, verdadeiro, do relógio a resposta é simples:     Mede-se o seu comprimento e aplica-se  a formula  de calculo  do comprimento do pêndulo.

 
Post de 04 Fev. 12  
 

CALCULO DAS  SEMI - OSCILAÇÕES   POR HORA   S / OSC / H

As semi - oscilações por hora ( s/osc./h ), são as alternâncias produzidas pelo balanço ou pelo pêndulo de um relógio, isto  as vezes que a ancora se move, no seu movimento alternado. 

No nosso exemplo anterior  verificámos que para uma volta da roda do centro a roda de escape daria  600 voltas.

N = Z1xZ2xZ3 / z2xz3xz4 = 80x75x60 / 10x10x6  = 600

Vamos agora supor que a roda de escape do relógio, em causa, tem 15 dentes. Porque cada dente da roda de escape dá sempre dois impulsos à âncora ( duas s/osc./h ), então  15 dentes x 2 = 30 impulsos .

Logo: 600 voltas x 30 impulsos / volta = 18.000 semi – oscilações por hora / alternâncias  ou ainda  300 alternâncias por minuto  ou  5 alternâncias por segundo . Trata-se obviamente de um relógio de  pulso,  bolso ou electrónico, mas não de um relógio  de  parede/mesa  mecânico, que são  muito mais lentos.

Por exemplo; o pêndulo de um relógio  mecânico  de precisão, com um metro de comprimento, faz um alternância por segundo,  60 por minuto ou 3600 por hora. 5 vezes mais lento do que o exemplo  anterior.     

Conclusão:   s / osc / h = Z1 x Z2 x Z3 x 2 : z2 x z3 x z4
Esta é formula que tem,  ao longo dos tempos, distinguindo os técnicos dos amadores  de  relojoaria mecânica


Post de 25 Nov. 11

6.2 - RAZÃO DE TRANSMISSÃO

Chama-se razão de transmissão ( P ),  à relação entre o número de dentes de uma roda e o número de dentes do carreto com a qual a roda engrena.

Assim: 

Se uma roda de  80 dentes engrenar com um carreto de 8 dentes, a respectiva razão de transmissão é  10, porque  P = 80 / 8 = 10.  Isto é: Para uma volta da roda o carreto dará  8 voltas.

O que é verdadeiro para a relação de uma roda com um carreto, também o é para um conjunto de engrenagens.

Assim,  se tivermos:

Z1 = 80; Z2 = 75; Z3 = 60;  z2 = 10; z3 = 10  e z4 = 6

Pergunta :

Quantas voltas ( N )  dará a última roda, quando a primeira roda  der um volta ?

Resposta:

N = Z1xZ2xZ3 / z2xz3xz4 = 80x75x60 / 10x10x6  = 600

Para uma volta  de Z1, Z4 dará 600 voltas .

Conclusões imediatas:

1-     As rotações são inversamente  proporcionais ao número de dentes.

2-     A aplicação de um ponteiro de segundo obriga a uma relação de 1 para 60 entre a roda do centro e a roda  dos segundos.

6.3 - APLICAÇÃO DE UM PONTEIRO DE SEGUNDOS

EXEMPLOS:

P - Poderá aplicar-se um ponteiro de segundos  numa relógio com as seguintes engrenagens : Z1 = 80 ; Z2 = 75; z2 = 10 e z3 = 10  ?

N = Z1 X Z2 / z2 x z3  = 70x71 / 10x10 = 60  voltas

R – Pode , porque a razão de transmissão é de 1 para 60 !

P – Poderá aplicar-se um ponteiro de segundos na situação seguinte : Z1 = 70;  Z2 = 70; z2 = 10 e z3 = 10  ?

N = Z1xZ2 / z2xz3 = 70x70 / 10x10  =  49 Voltas

R – Não pode, porque a razão de transmissão é de 1 para 49 e não de 1 para 60 !

Post de 11-11-11

6.0 - ENGRENAGENS DE RELOJOARIA

Na relojoaria existem, basicamente, dois tipos de engrenagens diferentes:

1- Engrenagens Roda – Carreto
2- Engrenagens Roda – Roda

No primeiro caso a força motora é sempre transmitida pela roda e a folga da engrenagem encontra-se no carreto pelo que, nas rodas, a espessura dos dentes e o espaço entre dentes é igual.

No segundo caso a transmissão da força é indiferenciada: Roda – Carreto ou Carreto – Roda. É exactamente o caso das minuterias ou engrenagens especiais. Nestas situações a folga da engrenagem encontra-se repartida pelas duas peças, sendo a espessura dos dentes menor que o intervalo entre eles.

Códigos para cálculo de rotações / transmissões:

Z -   número de dentes, em geral ou do tambor
Z1 - número de dentes da roda do centro
z1 -  número de dentes do carreto da roda do centro
Z2 - número de dentes da roda intermediária, também conhecida por roda 3ª
z2 -  número de dentes do carreto da roda intermediária
Z3 – número de dentes da roda dos segundos ou roda 2ª
z3 – número de dentes do carreto da roda de segundos
Z4 – número de dentes da roda de escape
z4 – número de dentes do carreto roda de escape

6.1 - Cálculo de uma roda perdida - MINUTERIA:

Minuteria, é o mecanismo que nos permite, através dos ponteiros, a indicação das horas e dos minutos. Por conseguinte existem minuterias de 12 e de 24 horas, consoante a relação ente o movimento dos ponteiros das horas e minutos é de 1 para 12 ou de 1 para 24 .

A minuteria é constituída por 4 peças essenciais:

1-“ Chaussé “ ou carreto ( C ), fixado no eixo da roda do centro, suporte do ponteiro dos minutos e órgão motor deste mecanismo.

 

2- Roda da minuteria ( M ), que engrena com o “ Chaussé “

 

3- Carreto da minuteria ( cM ), solidário com a roda da minutera

 

4- Roda de Horas ( H ), por no seu canhão, ser aplicado o ponteiro das horas.

Normalmente a relação de transmissão, entre o “ chaussé “ e a roda das horas é de 1 para 12, dado que a uma volta do ponteiro das horas correspondem 12 voltas do ponteiro dos minutos. Se o mostrador for de 24 horas, então aquela relação passa a ser de 1 para 24.

Para efeito de cálculo de qualquer uma daquelas 4 peças, num relógio com mostrador de 12 horas, deve usar-se a seguinte equação:
M = 12 x C x cM / H

Caso: Num relógio perdeu-se a roda das horas ( H ), fizemos uma contagem e verificámos o seguinte: C tem 20 dentes; M tem 40 dentes e cM tem 10 dentes. Quantos dentes deve ter a nova roda das horas ?

H = 12 x C x cM / M ou H = 12 x 20 x 10 /40 = 60

Resposta : Roda das horas deve ter 60 dentes




Post: Abr.03,11

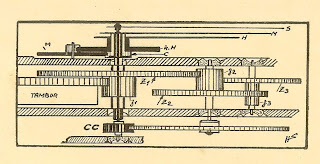
5.0 - ESTRUTURA DE UM RELÓGIO MECÂNICO

E estrutura actual de um relógio mecânico, que mostramos em baixo, está praticamente estabelecida desde há 300 anos.

5.1 Platinas
5.2 Fonte de energia motora
5.3 Transmissão ou engrenagens ( inclui sistema de minuteria )
5.4 Sistema de escape
5.5 Sistema de regulação
5.6 Sistema de informação

5.1- PLATINAS:

Em tecnologia de relojoaria, chamamos de platinas às peças (em barra ou em chapa ) que servem de apoio às engrenagens . Ao longo do tempo, as platinas também evoluíram bastante, tendo em consideração não só o seu aspecto estético mas principalmente devido à necessidade de redução do atrito, no movimento de rotação dos pivots dos eixos das rodas e carretos. Também a matéria prima usada na sua fabricação evoluiu, passando da madeira usada inicialmente, para o ferro fundido, o aço, o alumínio e finalmente o latão.





Platinas trabalhadas - UK




Exemplo de Platinas em madeira



Platinas em Ferro - Rel. Morez

Post: Mar.11.11

1.0-INTRODUÇÃO:

Esta pagina vai ser dedicada à Tecnologia de Relojoaria Mecânica, para ajudar os amadores de Relojoaria e entenderem como se chega ao projecto, construção e reparação das peças de uma máquina de relógios, autenticas obras primas de engenharia de mecânica de precisão.

Falaremos também das principais matérias primas utilizadas, cálculos, desenhos, construção e ideias para reparação de situações mais ou menos difíceis, como por exemplo o cálculo do numero de dentes de uma roda ou de um pêndulo perdidos ( coisas que os amadores desconhecem, mas que dá jeito conhecer !).

A relojoaria é conhecida pela profissão das mil e uma ferramentas, muitas delas construídas durante a aprendizagem da profissão, como método de educar os formandos a trabalhar com inteligência e paciência, duas condições necessárias para um desempenho profissional de qualidade.

2.0- MATERIAIS MAIS USADOS EM RELOJOARIA MECÂNICA

Várias tipos de aço ( eixos, pernos e cavilhas, molas, bordões, chaves, etc.); Latões ( rodas, platinas, bordões, mostradores e outros acessórios ); Cobre ( buchões, mostradores, acessórios decorativos ); Nikel ou ligas ( pêndulos de precisão ): Pláticos ( Rodas e carretos em Delrin começaram a ser usados a partir dos anos 60 do século XX ); Esmaltes ( mostradores e pelas decorativas); Madeira ( essencialmente no fabrico de todo o tipo caixas ).

2.1-AÇO

O aço é uma liga metálica formada, essencialmente, por ferro e carbono, onde as percentagens deste último elemento variam entre 0,01 e 2,1%. O chamado ferro forjado contém entre 0,02% e 0,05% de carbono e os aços mais utilizados em relojoaria contêm entre 0,5 e 1,7 % de carbono.

Convém ter presente que também o ferro fundido é uma liga de ferro e carbono, mas neste caso as percentagens de carbono variam entre 2,1% e 6,7 %.

A principal diferença entre ambos é que o aço, pela sua ductibilidade é facilmente deformável por forjamento, laminação e extrusão, enquanto que uma peça em ferro fundido é muito frágil para manobrar ou trabalhar.

Julga-se que a fabricação de peças em ferro tenha tido o seu início cerca 2000 a.C e a dita idade do Ferro tenha sido estabelecida por volta de1000 a.C. Neste período a tecnologia da fabricação do ferro espalhou-se pelo mundo. Os minérios de ferro eram abundantes na natureza, assim como o carvão, o que não acontece na actualidade. Hoje em dia, a maior quantidade de matéria prima para produção de provem dos resíduos da produção industrial.

O aço é uma das principais matérias primas da relojoaria, são várias as peças e ferramentas fabricadas em aço: Buris, brocas, alicates, pinças, alavancas, cavilhas, caixas, parafusos, chaves, molas, eixos, carretos, bordões, etc.

Ao analisarmos aquelas peças e ferramentas observamos que têm graus de dureza e flexibilidade diferentes , isso deve-se à capacidade que os aços têm de poderem receber tratamentos térmicos como a tempera e o revenido que lhe conferem aquelas características consoante a finalidade da peça ou da ferramenta.

2.2- COBRE – Cu

Conhecido, desde a antiguidade ( onde é hoje o Iraque, foi encontrado um colar de cobre de 8700 a.C. ), encontra-se na natureza em estado sólido, sendo um dos  metais mais  usados na produção industrial,  quer sob a forma  simples quer  na formação de ligas como é o caso do bronze e do latão. De cor avermelhada, o cobre  é dúctil e maleável e bom condutor de electricidade.

O cobre, em relojoaria , foi muito utilizado no fabrico de mostradores,  muitos deles esmaltados,  em relojoaria eléctrica e  pequenos acessórios.

2.3- ZINCO- Nn
 

Encontra-se na natureza  no estado sólido e  são conhecidas  ligas de zinco  em peças  datadas de 1400 a.C.  Efectivamente , o zinco foi desde sempre, um metal fundamental  produção de ligas metálicas  como o latão e o bronze, para além da sua  grande popularidade   na protecção de superfície de peças de  ferrosas.

Em relojoaria a utilização do zinco  resume-se fundamentalmente á produção de matéria prima em latão e bronze, para além  pequenas aplicações em caixas.   

Post: Mar.25.11

3.0 - EXEMPLOS  LIGAS NÃO FERROSAS

3.1 - BRONZE
 

O Bronze é uma liga  que tem como base o cobre e oestanho  aos quais  se adicionam  outroselementos ,  como  zinco, alumínio,  antimónio, níquel, fósforo , chumbo  entre outros,  sempre que se  pretenda   obter características superiores a do cobre. Por exemplo: o estanho  permite  aumentar a resistência mecânica e a dureza do cobre sem alterar a sua  ductibilidade.

Sua grande popularidade  ficou a dever-se  à sua enorme resistência estrutural, à nãocorrosão atmosférica , à facilidade de fundição e uma capacidade de acabamento que permite excelente polimento ( cor amarelo –ouro ).

O bronze possui características acústicas e de geração de ondas sinusoidais bastante puras e apresentando um timbre  bem distinto, tornando-se assim um metal excelente para a fabricação de instrumentos musicais como é o caso dos sinos   e dos gongos .

Em relojoaria o bronze  foi desde sempre muito utilizado  quer em ferramentas ( limas de polir ), quer  na produção de peças, como são os casos  de    buchões, devido  á sua  elevada  resistência ao desgaste, mostradores ,  e   peças  de som,  casos  dos   bordões e campainhas,   dos mecanismos  sonoros de horas.

3.2 - LATÃO
 

O latão é uma liga metálica de cobre  e zincocom percentagens deste último entre 3% e 45%. Por  vezes  adicionam-se  pequenas quantidades de outros elementos como alumínio  (Al),  estanho (Sn),  chumbo (Pb),  para  melhorar  algumas  características da  liga, tem uma cor amarelo metálica semelhante à  do ouro .

Em relojoaria , as aplicações do latão  são  muito abrangentes ; Rodas, platinas, pontes, mostradores e acessórios  diversos como parafusos, cavilhas, pernos etc.

Fora  da relojoaria  o Latão é uma mat´éria prima muito  usada quer em objectos de uso industrial quer  quer de ornamentação doméstica e joalharia. 

4.0 -NORMAS E TOLERÂNCIAS

O sistema de metrologia usado na relojoaria a que nos queremos referir ( dita relojoaria grossa ), regula-se pelas Normas ISO ( International Standard Organization ), nomeadamente no que concerne ás tolerâncias de ajustamento dimensionais para furos e eixos. Importante para, por exemplo; calcular o grau de liberdade de um pivôt ou um ajuste de cravação de uma roda no seu eixo. Em termos gerais podemos dizer que neste tipo de relojoaria as tolerâncias menores raramente, são inferires a 0,05 mm e os acabamentos de superfície variam entre o " mate " para platinas ( dois triângulos ) e o "polido " dos pivots( quatro triângulos).

TEORIA DAS TRANSMISSÕES POR RODAS DENTADAS- Video  do Youtube